开放合作研究团队第49期Seminar学习讨论会
2022年12月13日晚19:00—20:00，中山大学区域开放与合作研究院学习讨论会以线上的方式成功举行。本次学习讨论会由史红晨硕士生分享文献《Using Synthetic Controls: Feasibility, Data Requirements, and Methodological Aspects》，参加学习讨论会人员包括毛艳华教授、副研究员、博士后以及博士生和硕士生等，另有澳门科技大学、澳门城市大学博士生通过线上形式参与了本次学习讨论会。
Using Synthetic Controls: Feasibility, Data Requirements, and Methodological Aspects
Alberto Abadie
一、 介绍
合成控制方法最初是由Abadie和Gardeazabal(2003)以及Abadie, Diamond 和 Hainmueller(2010)提出的，旨在估计政策干预的效果。
基本思想是：当观察单位是少量的总体实体（国家或地区）时，未受影响的个体的组合往往比任何单独的未受影响的个体提供了更合适的（数据驱动）。假设存在一个实验组和多个控制组，实验组从某个时间点开始受到策略影响，而对照组始终不受到该策略影响。那么给每个对照组找到一个对应的权重，使得干预前各个对照组合成之后的合成对照组跟实验组足够相似，那么合成对照组在策略实施时间点之后的效果，就可以看做实验组在无干预情况下的“反事实”效果。也就是说，实验组在策略实施后效果与合成对照组在策略实施后的效果的差异，就可以看做是策略实施所带来的。
具体应用在了各个领域，在评估政策干预效果上，应用SCM方法的有：控烟政策（ Abadie, Diamond and Hainmueller，2010）、移民政策（Bohn, Lofstrom, and Raphael，2014）、税收政策（Kleven, Landais, and Saez，2013）以及最低工资（ (Allegretto et al.，2017；Jardim et al.， 2017；Neumark and Wascher，2017；Reich et al.，2017）等等。
二、 SCM模型
（一） 设定
1. J+1个单位，j=1为处理单位（实验组），j=2、3…..J+1为未处理单位的集合（对照组）；
2. 时间跨度为T，其中
为干预期；
3. 对于每个j，在 t 时期，可以观察到的的结果变量表示为
；
4. 同时对每个单位 j 存在一组预测因子（假设有 k 个）：
；则对于 J 个对照组存在
；
5. 定义假设
和
分别表示“受到”和“未受到”政策干预两种情况下的“潜在结果”则有实验个体（j=1）在干预后第 t 时点（t ∈T1）的处理效应：
6. 当t>T0 时有
，为了得到政策干预的效果需要估计（构造反事实）。
（二） 估计
1. 关于
：
给定J个控制组单位一个合理的权重w（权重被限制为非负且总和为1），由此拟合出未受到干预实验组的数据从而得出政策干预效果，即
，其中
为控制组最优权重。给定J个控制组单位一个最优权重
（权重被限制为非负且总和为1），由此拟合出未受到干预实验组的数据从而得出政策干预效果：
2. 关于
即给定一组非负常数
找到
，
使得
最小化，由此得出W（都为干预前数据）。
比较处理组国家特征变量与加权合成处理组国家特征变量的距离来判断权重矩阵的优劣（聂飞，2017）。
3. 关于
V反应了每个预测因子在干预后时期合成
构造
，让干预前的MSPE最小化（ Abadie，2010）
out-of-sample validation（样本外数据验证法）：
（1）将干预前的时期（简化分析假设
为偶数）分为初始处理（1-
）和后续验证期（+1-），其中=/2（在实践中，训练和验证周期的长度可能取决于应用特定因素，例如干预前和干预后阶段结果的数据可用性程度，以及在数据中测量预测值的特定时间）
（2）对每个V由处理期得出相应的最优权重，由此得出后续验证期的MSPE：
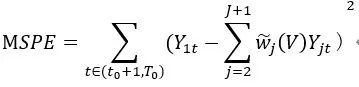
（3）让上述MSPE最小化得出
，用和后续期数据算出
。对后续验证期存在：
（三） 构造
生成：
• 使用Abadie et al．(2010)提出的因子模型来估计：
• 其中，δt为时间趋势项，Zj和μj分别为可观测和不可观测解释变量构成的向量，θt和λt为对应的时变参数向量，εjt为不可观测的随机冲击。
• 向量W的每个特定值表示潜在的合成控制，即控制区域的特定加权平均值。以W为权重的每个合成控制的结果变量的值为：
• 则对于
有：
• 值得注意的是，干预后的结果并未用于计算合成控制权重
（四） 检验
假设控制组国家也实施了该政策干预，实施合成控制，然后将实际的政策实施效果与控制组经济体假设的效果进行比较，如果两者的政策效果有足够大的差异，则说明政策的实施作用效果显著
具体做法：
• 构造RMSPE（RMSPE主要用以衡量处理组与其合成控制对象之间的拟合差异度，事件发生之前的RMSPE越接近于0，就意味着拟合差异度越小，合成控制对象越理想）：对于
，且
，有：
• 判断政策效果：
1、丢掉对照组里面pre大于post的国家，然后根据post判断政策效果
2、构造
，越大，说明政策效果越好，构造如下：
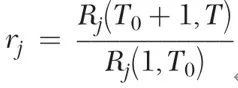
（五） 例子
以Comparative Politics and the Synthetic ControlMethod（Abadie，2015）文章为例。
• 时间跨度为1960-2003，干预年份为1990
• 对照组：一组工业化国家包括澳大利亚、奥地利、比利时、丹麦、法国、希腊、意大利、日本、荷兰、新西兰、挪威、葡萄牙、西班牙、瑞士、英国和美国（从1990年的23个OECD成员国中排除排除了卢森堡和冰岛（面积小，经济特殊）、排除了土耳其，（1990年的人均GDP水平远低于抽样中的其他国家）、排除了加拿大、芬兰、瑞典和爱尔兰（在样本期间受到深刻的结构性冲击的影响））
• X预测因子为：一套标准的经济增长预测指标（西德人均GDP（1981-90年期间的平均数），通货膨胀率，行业增加值份额，投资率，学校教育和贸易开放程度）
• Out-of-sample验证法：1971—1980年的处理期和1981—1990年的验证期，选择V使得验证期：
• 或MSPE最小化（使用处理期的预测因子以及得到的W）
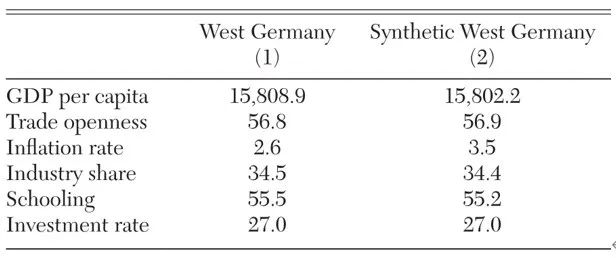
• 得到结果为（V）：是人均 GDP （0.442）、投资率 （0.245）、贸易开放度 （0.134）、学校教育 （0.107）、通货膨胀率 （0.072） 和行业份额 （0.001），如下图：
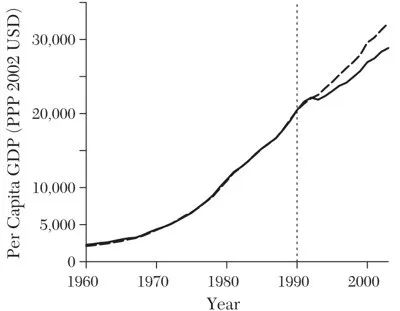
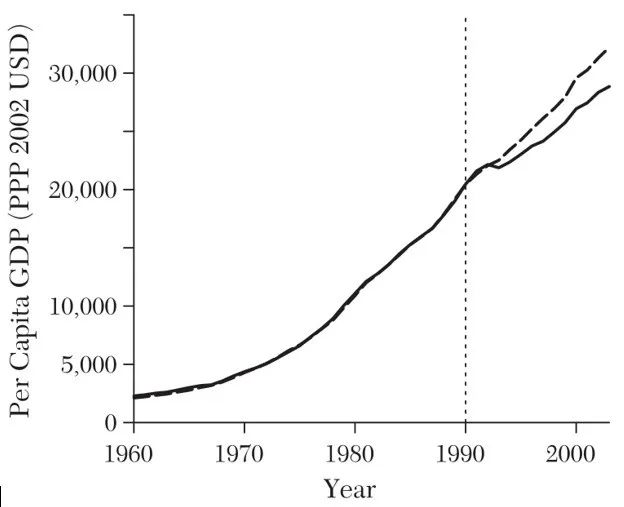
实线为西德真实数据，虚线为合成控制，这一图像表明，对照组国家的合成控制能够接近德国统一前西德人均GDP的轨迹，且完美重现了西德经济增长预测的回归前值。
据表格显示，对于预测因子，可以看出合成控制提供了相当精确的近似值
统计检验：
In-time：即把干预提前并进行合成控制，如果提前后的时间点到策略真实作用时间点之间，合成控制组和实验组差异不显著，则说明通过In-time placebo。
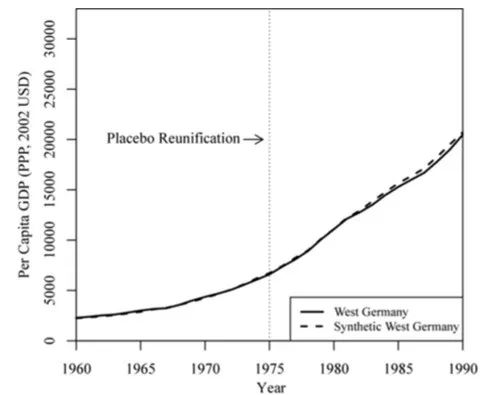
合成的西德几乎完全再现了1960-1975年期间实际西德人均GDP的演变。西德及其合成国家的人均GDP轨迹在1975-1990年期间没有太大差异，说明政策有效。
In-space：即假设控制组国家也实施了该政策干预，实施合成控制，如果西德的估计效应相对于安慰剂效应的分布异常大，则政策显著。
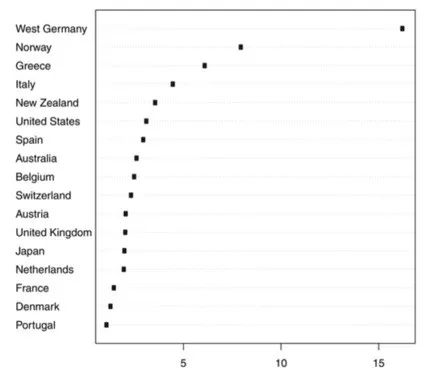
上图显示了为各国实施干预后的图，西德显然是RMSPE比率最高的国家，因此德国统一对西德影响显著。
三、 SCM的优点
（一） Preclude extrapolation
1. 权重非负且和为一
2. 线性回归使用外推法来确保处理单元的特性完美拟合，即使未处理单元的特征与处理单元完全不同（即使完全不同也能完美拟合）
（二） Transparency of the Fit
1. 合成控制使实验组和对照组之间的实际差异透明
2. 可以反映：
1) 每个控制组单位对合成控制的相对贡献
2) 就干预前结果和干预后结果的其他预测因素而言，受关注事件或干预影响单位与合成控制组之间的相似性
3. 德国统一的例子：
（三） Safeguard against Specification Searches
合成控制不需要在研究设计阶段获得干预后的结果：
1.所有关于设计决策的数据分析，如对照组中权重为正的控制组单位的确定或X1和X0中的预测因子，都可以在不知道它们如何影响研究结论的情况下进行
2权重可以在干预后结果实现之前或在实际干预发生之前计算得出（干预后的结果并未用于计算合成控制权重）
（四） Transparency of the Counterfactual
1. 明确给出每个控制组单位的权重
2. 权重适当而稀疏（并非所有国家都有权重），因此可以对反事实估计的性质进行一个准确的解释
（五） Sparsity
1.德国统一的例子：
西德的反事实由奥地利（0.42）、日本（0.16）、荷兰（0.09）、瑞士（0.11）和美国（0.22）的加权平均值给出
2.为什么德国统一会导致西德人均GDP的下降
那是因为西德的较小邻国，如奥地利、荷兰和瑞士，对西德人均GDP的合成控制的组成有很大的影响。这些国家的经济增长在1990-2003年期间受到德国统一的负面影响（可能是因为西德将这些国家的需求和投资转移到了东德）
1. 简单线性回归因为允许外推里面所有的国家都有权重，因为外推，但是合成控制只有少数几个国家有权重。
2. 一般来说，预测因子的数量k比非零权重数量要多，因为实际实验组的预测因子落在合成控制的集合之外。
3. 以德国统一为例：权重为正国家数量为5，预测因子数量为6。
四、 变量和数据要求
（一） 变量要求
1.Size of the Effect and Volatility of the Outcome：
• 干预措施的影响小，无法与其他冲击加以区分，如果结果的波动性也很大，即使是影响很大也很难检测到
• 通过过滤消除波动性
2.Availability of a Comparison Group：
• 排除有相似政策干扰的控制组单位
• 排除研究期间那些遭遇重大冲击并可能对合成结果产生影响的控制组单位
• 选取具有相似特征的控制组
3.No Anticipation：
• 如果前瞻性经济行为体在调查的政策干预之前做出反应，或者如果干预的某些组成部分在干预的正式实施/颁布之前到位，则合成控制估计可能会有偏差
• 排除有预期影响的情况
• 如果有预期作用，合成控制时，将干预时间提前到预期发生前
4.No Interference：
• 没有政策溢出效应
• 一般处理方法是排除受到政策溢出效应影响的单位
5.Convex Hull Condition：
• 避免预测因子某一变量的极端值情况（难以合成）
• 极端值处理：
（1）轨迹拟合很好的个别极端值情况，无需处理
（2）受干预影响的单位在干预前的结果变量的可能极端值导致拟合不好的情况，可以考虑转换成：
或者增长率：
6.Time Horizon：
• 一些干预措施的效果可能需要时间才能显现出来，或者需要足够的时间才能在数据中定量检测到
• 等到干预的效果发挥作用；使用替代结果或结果变量的领先指标
（二） 数据要求
1.Aggregate Data on Predictors and Outcomes：
• 可以从政府机构、多边组织和私人报告获取
• 也可以采用更微观层面数据的加总
2.Sufficient Pre-intervention Information：
• 合成控制估计的可信度在很大程度上取决于其在干预前结果变量和合成控制的拟合情况，因此充足的干预前信息至关重要
3.Sufficient Post-intervention Information：
• 广泛的干预后信息可以更全面地了解干预的效果
五、 拓展延伸
（一）Multiple Treated Units
• 多个处理单元的情况下使用合成控制进行估计和推断
• 可参考文献：
1、A Penalized Synthetic Control Estimator for Dissagregated Data（ Abadie and L ’Hour ，2019）
（二）Bias Correction
• K合适但无法很好拟合（处理单位的与相应合成对照的预测因子之间的匹配差异所产生的潜在偏差）
• 可参考文献：
1、 A Penalized Synthetic Control Estimator for Dissagregated Data（ Abadie and L ’Hour ，2019）
2、 Synthetic Difference in Differences（Arkhangelsky et al. ，2019）
3、 Practical and Robust t-Test Based Inference for Synthetic Control and Related Method（Chernozhukov et al. ，2019）
4、 The Augmented Synthetic Control Method（Ben-Michael et al. ，2020）
（三）Regression-Based Methods and Extrapolation：
• 允许外推
• 可参考文献：
1、Balancing, Regression, Difference-in-Differences and Synthetic Control Methods（Doudchenko and Imbens ，2016）
2、Synthetic Difference in Differences（Arkhangelsky et al. ，2019）
（四）Matrix Completion/Estimation Methods：
• 可参考文献：
1. 非线性因子结构模型：Robust Synthetic Control（ Amjad, Shah and Shen 2018）
2. 假设所有变量都取决于共同潜在因素：Matrix Completion Methods for Causal Panel Data Models（Athey et al.，2020）
（五）Inference：
• 在in-time和in-space的基础上拓展
• 可参考文献：
1. Synthetic Control Method: Inference, Sensitivity Analysis and Confidence Sets（ Firpo et al.，2018）
2. Synthetic Control and Inference（Hahn and Shi ，2017）
3. An Exact and Robust Conformal Inference Method for Counterfactual and Synthetic Controls（Chernozhukov et al.，2019）
4. Prediction Intervals for Synthetic Control Methods（Cattaneo et al.，2021）
（六）Other Contributions：
• 可参考文献：
1. Regional Policy Evaluation: Interactive Fixed Effects and Synthetic Controls（ Gobillon and Magnac ，2016）
2. Synthetic Learner: Model-Free Inference on Treatments over Time (Viviano and Bradic，2019）
3. Distributional Synthetic Controls（Gunsilius ，2020）
六、 讨论与建议
研究院成员对文献分享展开了有关讨论。毛艳华教授与荣健欣副研究员与认为本篇综述文章适合做应用计量的人士进行学习。在应用方法时，要考虑方法的适用性和应用边界，可以通过学习一些顶刊文章，来仔细探讨各种计量方法的适用背景。
文献分享结束后，毛艳华教授与相关成员进行项目进度以及工作内容讨论。本次学术研讨会充分体现了研究院浓厚的学术氛围，大家在学术交流中相互学习、共同进步，提高自己的学术能力，至此，本次学习讨论会圆满结束。
拟稿：蔡儒雅
编辑：陈多多
审核发布：毛艳华