开放合作研究团队第8期Seminar学习讨论会
2021年7月6日晚19:00-20:30,中山大学区域开放与合作研究院文献研读会议以线上方式成功举行。本次学习讨论会由李子文博士分享文献。参加学习讨论会人员包括毛艳华教授、李兵副教授、副研究员、博士后以及博士生和硕士生等,另有澳门科技大学、澳门城市大学博士生通过线上形式参与了本次学习讨论会。

The Gravity Equation in International Trade: An Explanation
Thomas Chaney

一、研究背景
引力模型方程自1962年提出以来,经过不同方法,不同国家样本的检验,仍然保持惊人的稳定性,是经济学中最有力的经验规律之一。引力方程显示,两个国家的贸易量与GDP成正比,与两国距离成反比。现有文献已经清晰地解释两个国家的贸易量与GDP成正比这一关系,但两个国家的贸易量与两国距离成反比仍然缺乏较为清晰的理论解释。现有文献将地理距离视作运输成本、政治差异、文化差异等贸易壁垒。然而,随着全球交通通讯技术的提升,引力方程中两个距离对贸易的影响系数依然稳定。这意味着对于两国家的贸易量与两国距离成反比这一关系的还有更深层次的理论解释。
二、理论框架
该文首先建立一个垂直的产业链模型。市场上只有中间品和最终品两种产品。最终品由当地中间品投入生产,并在当地销售,处于完全竞争市场。而中间品则由中间品和劳动投入生产,全球分布,且仅中间品可以贸易。同时,设定全球相同的固定工资w,人口增长率也为常数γ。中间品企业的产品价格则为边际成本加上溢价(如式(4))。

此外,该文提出关键的一个假设,就是对称性假设。假设一条产业链上的企业拥有相同数量的供应商和客户,每家企业的产品价格是一样的。
企业的销售量则有中间品销售和最终品销售两部分组成(如式(5))。这意味着企业的销量跟供应商数量和客户数量相关。
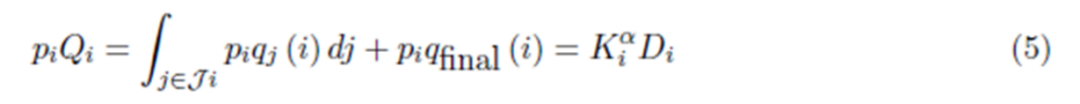
该文假定每家企业收取的溢价是固定的,且在对称性假设下,拥有K个供应商的企业只会与也有K个供应商的企业交易。因此,均衡下,企业的销售价格就相当于其支付给供应商的价格(如式(6))。
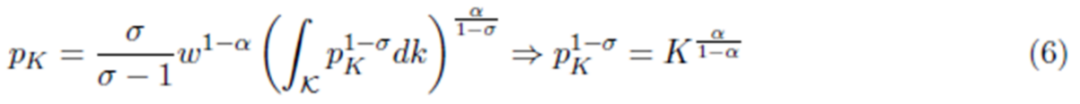
均衡总价则是结合企业的累积分布情况,其中M为每个地点企业分布数量的测度(如式(7))。
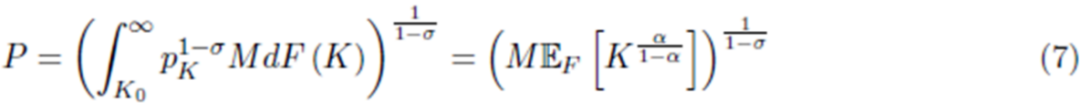
均衡总价格与企业数量呈负相关关系,企业数量越多,效率越高,价格越低。
均衡的总销售量则如式(8),中间品运输量则如式(9)。
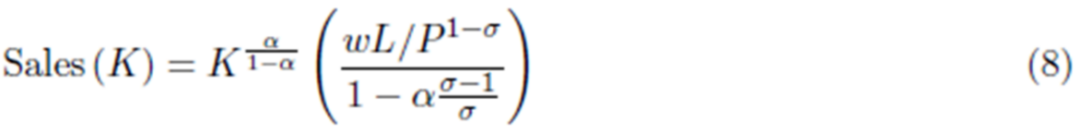
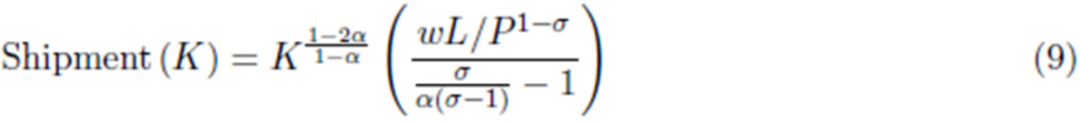
该文在以上垂直生产链模型中加入供应商信息买卖市场。假设企业初创时会带有一定的供应商和客户。企业会积极地从现有的供应商里购买供应商的上游供应商信息,从而壮大自己的供应商数量。企业也会向下游客户销售自己拥有的供应商信息,从而构成一个自上游往下游的信息销售链(如图1)。
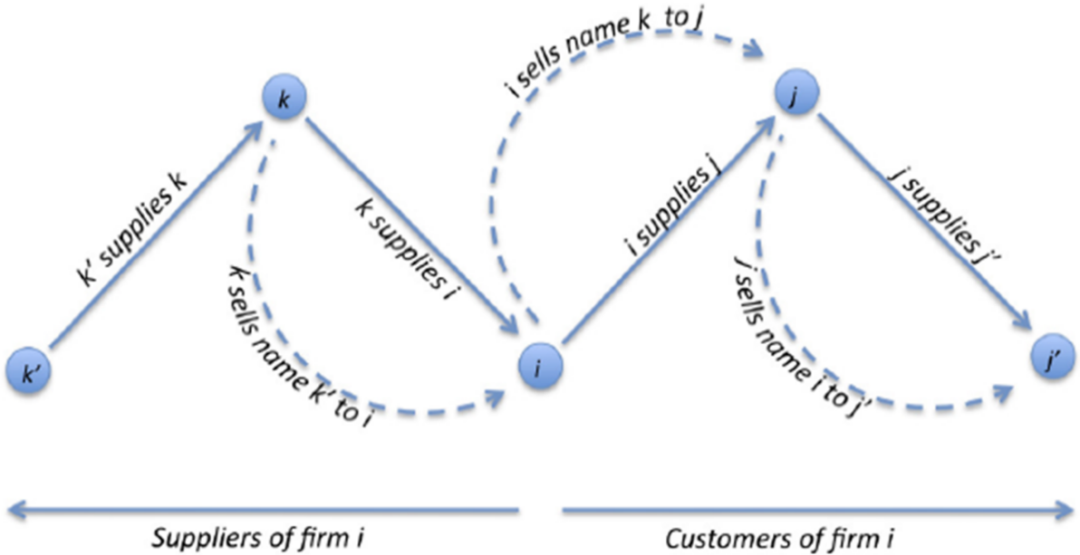
图1 供应商信息的买卖模式
该文也设定一个修正成本函数![]()
,其中I为购买供应商信息的投入,也设定供应商数量存在一个固定损失率δ,以及一个固定的增长率β。因此,企业的收益则由四部分组成,一是产品销售收入,二是供应商信息购买支出,三是供应下信息出售收入,四是修正成本函数支出(如式(10)。其中修正成本函数,是与供应商的数量成反比,意味着企业为了降低成本有动力去不断扩大自己供应商的规模。该成本函数的所刻画的是企业为了引入新供应商而调整生产过程或者投入结构所带来的成本。
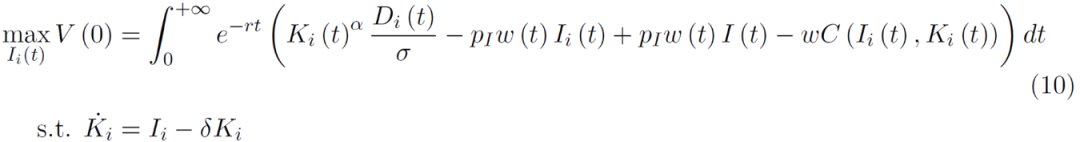
对式(10)进行一阶求导,解出新增供应商投资与现存供应商的关系,即企业为了新增供应商的最优投资策略(如下式)。
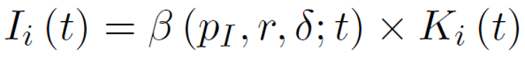
供应商的新增比率固定为β,根据上面式(8),企业每期收益为1/σ,而且进入成本设定为。因此,只要企业的折现收益高于进入成本,即可自由进入市场,如式(11)。
![]()
当新企业进入市场后,其供应商净增长为:
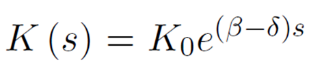
为了增加新供应商获取信息而投资为:
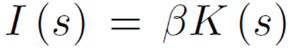
基于修正函数的齐次性,修正函数可变为:
![]()
人口增长率为γ,即
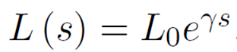
均衡增长下,企业也会以增长率γ速度增长。
上文均衡总价格公式(7)可以改写为:
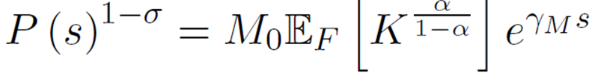
结合自由进入条件式(11),可得均衡增长路径,如式(12):
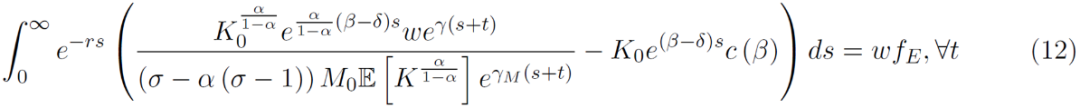
该文章不仅给出了模型的静态均衡,也给出了动态均衡结果。市场上企业的数量会以人口增长率γ速度增长。新创企业会自带一定数量的供应商和客户。以随机方式,企业会增长β比率的供应商和减少δ比率的供应商(γ>β-δ>0)。企业规模与其供应商的数量成正比。
该文在以上的垂直产业链模型中引入,地理空间的概念,设定企业分布在无限一维连续空间,线上的每一个坐标代表一个城市,国家就是城市的集合。企业诞生时的供应商K0的地理分布是由概率密度函数g0(.)决定,在两个地点[a,b]间的K0为:
![]()
是一家企业在t时刻供应商的地理分布,是指这家企业的供应商总数量,标准化的就是这家企业供应商分布的概率密度函数(如式(13))。
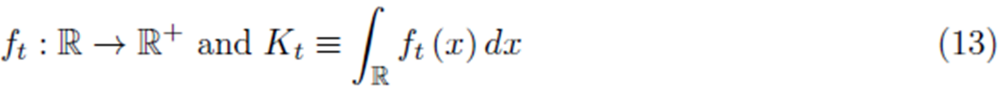
企业的供应商按照以下偏微分方程递归演化:
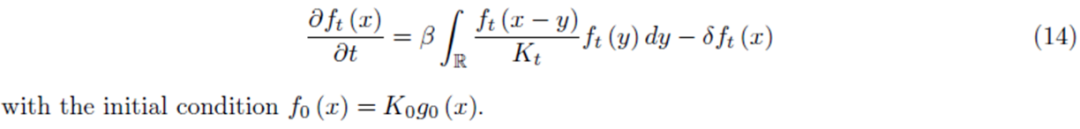
x和y是指地点,等式左边是在dx上新供应商净增长,等式右边就是供应商的新增减去消失。
随着企业经营时间增加,其供应商数量也不断增加,如式(15)。
![]()
该文认为当一个企业的供应商数量和市场上企业数量都呈指数增长时,模型预测供应商数量在人口中的分布是帕累托分布的。
年轻企业的供应商比老企业少,人口增长率γ越大,年轻企业越多,相对来说拥有大量供应商的企业越少。供应商增长率β越大,老企业的供应商数量越大。供应商的净增长率β-δ越高,越多供应商数量大的企业。式(16)表示供应商数量为K的企业的占比。
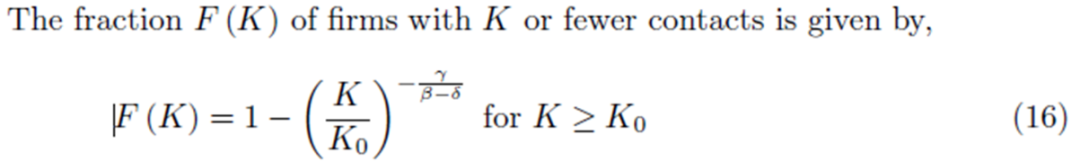
该文假设每一家初创企业都有一定的初始供应商,且与这些供应商有一定的距离,设初始平均距离为:
![]()
此外,该文还有一个重要假设,即假设初创企业只跟同时期的企业购买供应商信息。企业离自己的供应商有一定距离,供应商离自己的供应商也有一定距离,如此类推。所以,随着企业不断向自己的供应商购买新供应商信息,该企业的供应商分布距离会不断增大,供应商分布越分散。为企业与自己供应商的平均距离,如式(17):
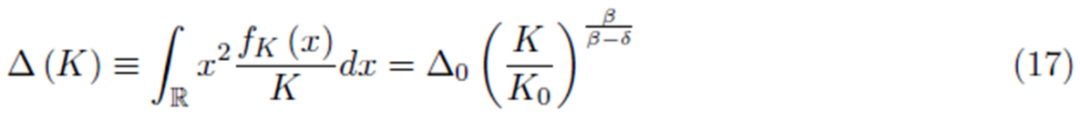
该文还给企业的供应商地理分布推导出一个特殊的渐近性质,t足够大,供应商的地理分布渐近于拉普拉斯分布。随着企业发展,其供应商的所在位置受到距离的影响越来越少。即便地点x离y很远,但x分布的供应商数量与y相当。

在简化假设下,中间产品在生产中所占的份额是一半,所有的发货量都是相同的,一个企业向每个下游企业出口一批货。两个地点之间的贸易量,无论是在企业还是在总水平上,都与这些地点之间的货物数量成简单的比例。
初始供应商的概率密度函数是对称的,且是有限方差,可得引力方程:

进一步,该文提出,如果单个企业之间的出口规模分布接近齐夫定律,那么两国之间的总贸易流量大致与各自的规模成正比,与它们之间的距离成反比,引力方程也成立,并且距离的弹性系数接近-1。

总的来说,该文基于供应商的地理分布随时间增加而不断分散的规律,推导出人口增长率越高,相对于老企业,新企业增加得越多,即新企业占比高,且新企业只能与距离较近的企业进行贸易。因此,在总贸易上,与距离成反比。此外,新供应商增长率越低,更少企业会去建立远距离的供应商,企业层面或总贸易上,与距离成反比。新供应商的消亡率则反之。
随后,该文进一步放松了一部分假设,整体结论并没变化,验证了理论模型的稳健性。此外,该文还推导了贸易中断,在长短期上对福利的影响效应,认为贸易中断,在短期上对应总福利造成巨大的损失,特别是老企业规模大的情况,供应商分布距离越远,损失越大,重建产业链成本越高。此外,高人口增长率,新企业加速进入会加快贸易中断后整体向均衡增长的恢复。
三、实证检验
该文在实证检验上相对较为简单,采用1992年法国的企业层面的出口数据,而在地理距离测定上则是在法国周围画一个500公里的同心圆,计算每一个圆中至少出口一个国家的法国出口商总数,以此来测定距离。最后,用OLS模型进行估计:
![]()
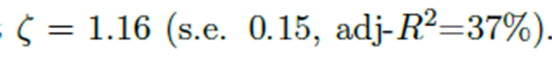
可以看出,地理距离是系数是接近于-1,理论模型的预测是成立的。该文进一步地采用了部门数据样本进行检验,结论同样稳健。
四、结论
该文建立一个垂直产业链模型,引入地理空间概念,特别为引力方程中,地理距离的影响提供新的理论解释。该模型认为企业的供应商分布距离是随时间增加而变长。因此,交通通讯等技术的进步虽然可以减少地理距离带来的物理成本,但是并没有缩短供应商分布的地理距离。引力方程中地理距离的影响系数在长时间内仍然稳定接近于-1.
文章分享结束后,团队成员在线上展开了热烈的讨论。李兵老师认为,该模型中的部分理论可以用来研究地震等自然灾害冲击后的生产恢复效果,但由于该文章所构建的理论模型整体上较为抽象,很难用来做相关的实证研究。其他成员也表达了相关看法,认为可以考虑利用该理论研究数字贸易领域相关问题,但在数据方面会受到一定限制,需要获得一些更微观的企业层面的相关数据。
本次学术研讨会充分体现了研究院浓厚的学术氛围,大家在学术交流中相互学习共同进步,提高自己的学术能力,至此,本次文献研讨会圆满结束。
拟稿:李子文、马帅兵
编辑:陈多多
审核:李兵
审核发布:毛艳华
