开放合作研究团队第45期Seminar学习讨论会

2022年11月15日晚19:00-20:30，中山大学区域开放与合作研究院学习讨论会以线上的方式成功举行。本次学习讨论会由张李世龙硕士生分享文献《Instrumental variable estimation of a spatial dynamic panel model with endogenous spatial weights when T is small》。该文于2016年发表在《Econometric Journal》期刊上。参加学习讨论会人员包括毛艳华教授、荣健欣副研究员、博士后以及博士生和硕士生等，另有澳门科技大学、澳门城市大学博士生通过线上形式参与了本次学习讨论会。

Instrumental variable estimation of a spatial dynamic panel model with endogenous spatial weights when T is small

Xi Qu, Xiaoliang Wang, Lung‐fei Lee

一、摘要与文献综述

（1）摘要

空间动态面板数据（SDPD）模型是分析具有空间相关性和经济单位之间动态依赖性的数据的标准工具。传统的估计方法依赖于空间权重矩阵是外生的这一关键假设，这在一些空间权重由经济因素决定的经验应用中很可能被违反。

在本文中，我们提出了一个短时维度的个人固定效应的SDPD模型，其中空间权重可以是内生的和时变的。文章建立了两阶段工具变量（2SIV）估计器的一致性和渐进正态性，并利用蒙特卡洛模拟研究其有限样本特性。

在应用这个模型研究中国的政府支出时，我们发现了中国省级政府在做出支出决策时存在空间相关性和时间依赖性的有力证据。

（2）文献综述

固定效应或随机效应空间面板估计的文献：

Elhorst (2005), Korniotis (2010), Su and Yang (2015), Yu et al. (2008, 2012) 和 Lee and Yu (2010) 研究了含固定效应的静态或动态面板。Mutl and Pfaffermayr (2010) 和 Lee and Yu (2012a) 研究了同时含固定效应或随机效应的空间面板，同时提出了空间模型的类 Hasuman 检验。Lee and Yu (2012b) extend Yu et al. (2008) 研究了含有随时间变化空间权重的空间面板。

考察空间权重内生性的文献：

Kelejian and Piras (2014) 使用 2SLS 估计控制短面板的内生性，但是其估计量的一致性预设了很高要求的假定。Lee (2015) 研究了含内生性空间权重的截面 SAR 模型，发现忽略内生性问题会对估计值产生实质性影响。Qu et al. (2017) 研究了空间长面板的 QML 估计量，其估计方法相当复杂，且要求空间权重必须被人为设定稀疏。

二、模型设定

本文要估计的含个体固定效应和内生空间权重的SDPD模型如下：

其中，和为n维向量，为均值0方差的独立同分布扰动项；为n x k1维控制变量矩阵；为n x n维的空间权重矩阵，为p维向量，且和的经济冲击影响（内生性来源）。

为了控制2.1中的内生性，本文引入了如下的辅助回归：

其中，为n x p维矩阵；为n x k2维控制变量矩阵；为n x p维扰动项矩阵，每一项均值0，但不需要同分布，方差矩阵主回归和辅助回归的扰动项属于同一联合分布，满足：

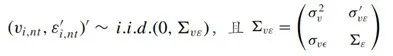
2SIV的主要思路是先估计辅助回归，并将辅助回归的残差代入主回归，由此可以利用控制住空间权重矩阵的内生性。具体来说，代入辅助回归的残差后，主回归变为：

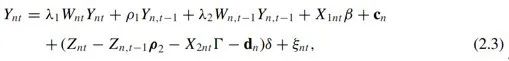
新的扰动项和方程中所有回归子都不相关，因此内生性问题可以得到控制。

三、估计方法

文章使用两步法估计该SDPD模型，引入标记和，设主回归的待估参数为。

（1）第一步：

（2）第二步：

文章证明，在选择合适工具变量的情况下，2SIV得到的估计量是渐近一致的：

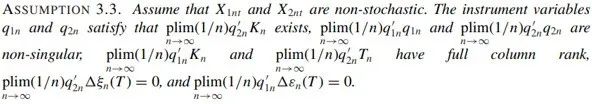
文章同时给出，满足Assumption 3.3 的一组工具变量为：

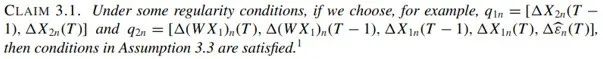
上述工具变量的一致性需要满足如下正则性条件：

作者通过证明 T<N 假定下， Jenish and Prucha (2012) 对空间数据的大数定理依然成立，说明以上正则项条件能够得到满足。但当 T>N 时，自相关无法忽略，此时 Jenish and Prucha (2012) 的 LLN 不成立，这个2SIV方法的估计量是不一致的。

（3）方差-协方差矩阵：

文章证明，待估参数的方差-协方差矩阵为：

对方差-协方差矩阵的一致估计量为：

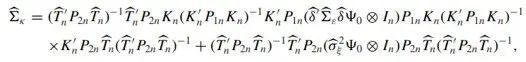
文章同时给出的一组一致估计量为：

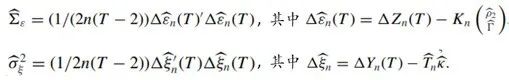
四、蒙特卡洛模拟

文章使用蒙特卡洛模拟探究小样本性质，DGP（数据生成过程）为：

主回归的参数的初值为：

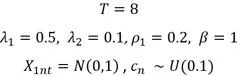
空间权重矩阵、辅助回归的DGP和参数为：

蒙特卡洛模拟的结果为：

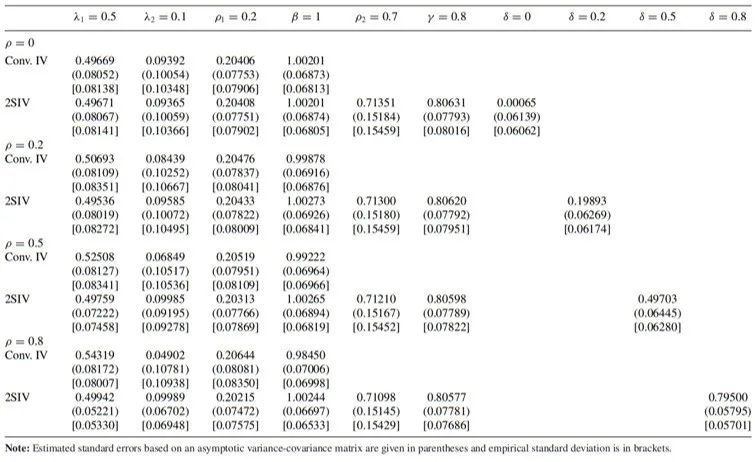
根据该模拟结果，2SIV估计量在小样本下是无偏的。

五、实证应用

文章为此2SIV估计方法进行了实证应用。实证背景为探究中国省级财政支出是否受到相邻省份支出的影响。由于官员晋升主要评估标准是当地与过去和其他省份相比的人均GDP增长率，作者预期不同省份在财政支出上存在竞争关系，因此设定了空间计量模型研究这种关联。

实证中的空间权重设定如下：

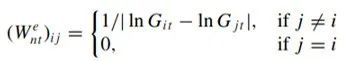
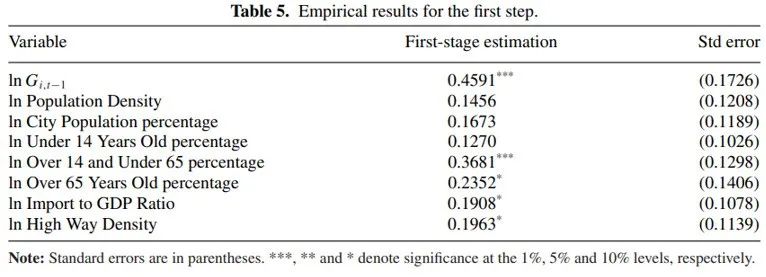
实证的第一步回归结果为：

实证的第二步回归结果为：

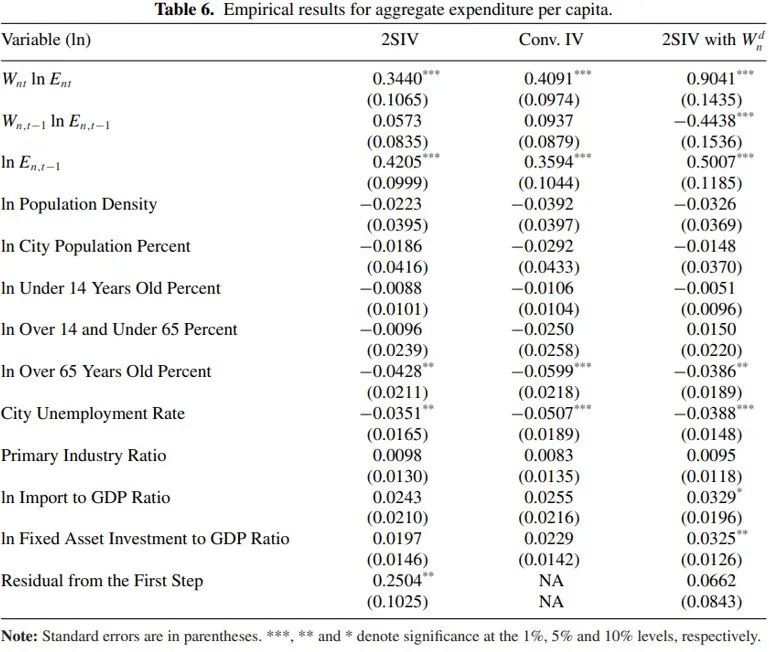
根据该回归结果，当空间权重矩阵与经济变量相关时，第一步的残差影响显著，表明此2SIV方法可以成功控制空间权重的内生性。

六、讨论

文章分享结束后，研究院成员展开了有关讨论。荣健欣副研究员询问了应用本篇文献方法的相关实证论文，认为做实证时重要的是理解新的方法做了哪些改进，有哪些新的应用场景；卓乘风博士后认为过去国内的空间计量研究对于空间权重矩阵的选择有主观性，且大都是静态的，不同区域的经济关联是随着时间变动的，因此这篇文献有比较广泛的应用价值。

本次学术研讨会充分体现了研究院浓厚的学术氛围，大家在学术交流中相互学习、共同进步，提高自己的学术能力，至此，本次文献研讨会圆满结束。

拟稿：李世龙

编辑：陈多多

审核发布：毛艳华